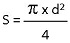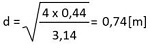Sauf prescription de votre formateur, en formation de niveau 3 (CAP), on n'étudiera pas ce chapitre .
Pour une unité de temps qui peut être l'heure ou la seconde, le débit correspond au volume généré par le déplacement dans une section qui se déplace à une vitesse donnée.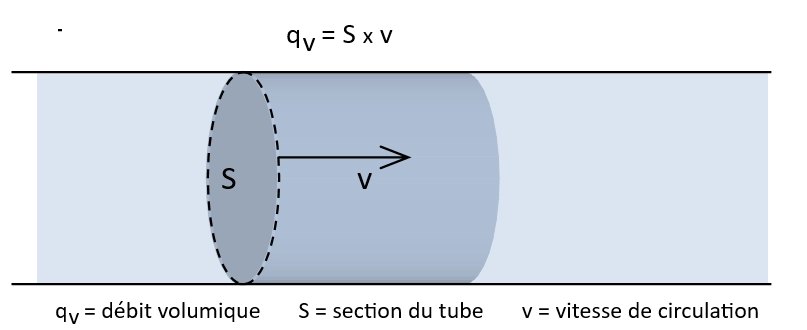
Le débit d'eau dans une canalisation se détermine par la multiplication de la section du conduit par la vitesse de circulation de l'eau.
Soit : Les vidéos récapitulatives de Maurice.
Dans notre branche professionnelle la formule "qv = S x v" se retient et s'utilise plus généralement sous la forme :
qv = v x S
Avec
qv = débit volumique en [m³/s]
v = vitesse du fluide en [m/s]
S = section de passage en [m²]
La formule nous permet de comprendre que pour une section de canalisation "S" donnée, plus la vitesse de passage "v" est grande, plus le débit d'écoulement "qv" est important.
Remarque
Cette formule peut donner lieu à ce qu'on appelle une "équation aux dimensions". Ce type d'équation consiste à remplacer les grandeurs physiques d'une formule par leurs unités.
La justesse de l'égalité obtenue permet de vérifier que la formule est juste. Soit, pour qv = v x S, l'égalité suivante.
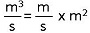
On constate ci-dessus que l'égalité des unités ci-dessus est juste. La formule qv = v x S est donc bien cohérente.
Cette formule qv = v x S est très importante. Elle nous permettra de déterminer le débit dans un conduit de section connue, si l’on arrive à y mesurer la vitesse de circulation du fluide en mouvement.
Dans le cas des gaines de distribution d'air, la vitesse de l'air en mouvement se mesurera grâce à un anémomètre.
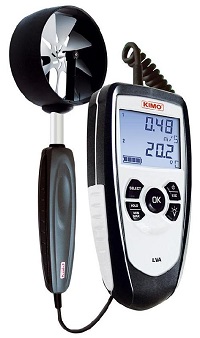
Anémomètre à moulinet (Source Kimo)
Question
Quel est le débit en circulation en [m3/s] et en [m3/h] ?
1,58 [m3/s]
5698 [m3/h]
Explication
Surface (section) = 0,71² x 3,14 / 4 = 0, 3957 [m²]
qv = 0, 3957 x 4 = 1,5828 [m3/s]
Soit 5698 [m3/h]
Question
Quel est le débit en circulation en [m3/s] et en [m3/h] ?
0,098 [m3/s]
352,80 [m3/h]
Explication
Surface (section) = 0,25² x 3,14 / 4 = 0,049 [m²]
qv = 0,049 x 2 = 0,098 [m3/s]
0,098 x 3600 = 352,80 [m3/h]
Observation
Tous les résultats sont arrondis à 2 décimales.
La formule qv = v x S peut se mettre en forme pour calculer la vitesse de circulation d'un débit connu qv, dans une gaine de section S.
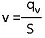
Avec
qv= débit volumique en [m³/s]
v = vitesse du fluide en [m/s]
S = section de passage en [m²]
Question
4,17 [m/s]
Explication
Débit qv = 4500 / 3600 = 1,25 [m3/s]
Surface = 0,5 x 0,6 = 0,3 [m²]
Vitesse v = 1,25 / 0,3 = 4,17 [m/s]
Question
5,67 [m/s]
Explication
S = 0,5² x 3,14 / 4 = 0,196 [m²]
Débit qv = 4000 / 3600 = 1,11 [m3/s]
Vitesse v = 1,11 / 0,196 = 5,67 [m/s]
Question
1,98 [m/s]
Explication
S = 0,25² x 3,14 / 4 = 0,049 [m²]
Débit qv = 350 / 3600 = 0,097 [m3/s]
Vitesse v = 0,097 / 0,049 = 1,98 [m/s]
Appliquons la formule à un rétrécissement.
Les vidéos récapitulatives de Maurice.

La formule qv = v x S peut se mettre en forme pour calculer la section d'un conduit permettant de véhiculer un débit connu, à une vitesse donnée.
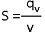
Avec
qv = débit volumique en [m³/s]
v = vitesse du fluide en [m/s]
S = section de passage en [m²]
Question
Quelle sera en [m2] la section de la gaine ?
Sachant que sa hauteur sera de 700 [mm], quelle sera en [m] la largeur de la gaine ?
0,694 [m²]
0,99 [m]
Explication
qv = 15 000 / 3600 = 4,167 [m3/s]
S = 4,167 / 6 = 0,694 [m²]
Nous savons que la surface est égale à la largeur x hauteur.
La hauteur étant de 0,7 [m] nous pouvons en déduire la largeur.
0,694 / 0,7 = 0,99 [m]
Question
Quelle sera en [m2] la section de la gaine ?
Quel sera en [m] le diamètre de la gaine ?
0,1944[m²]
0,49 [m]
Explication
qv = 2800 / 3600 = 0,778 [m3/s]
S = 0,778 / 4 = 0,194 [m²]
Nous connaissons la formule de la surface d'un cercle.
En transformant la formule, nous pouvons donc déduire le diamètre de la gaine.
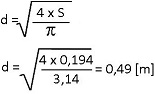
Question
Quelle sera en [m2] la section de la gaine ?
Quel sera en [m] le diamètre de la gaine ?
0,44 [m²]
0,75 [m]
Explication
qv = 9500 / 3600 = 2,639 [m3/s]
S = 2,639 / 6 = 0,44 [m²]
Comme dans l'exercice précédent, une fois la section connue nous pouvons trouver le diamètre.