N°3 - Relation puissance, débit et écart de température d'eau - niv. 3

La relation entre débit, puissance et écart de température d’eau s'exprime grâce à la formule suivante.
P = q_v × 1,16 × ΔT
Avec
P en [kW]
q_v en [m³/h]
1,16 = chaleur volumique de l’eau en [kWh/m³.K]
∆T = écart de température reçu ou perdu par l’eau en [K]

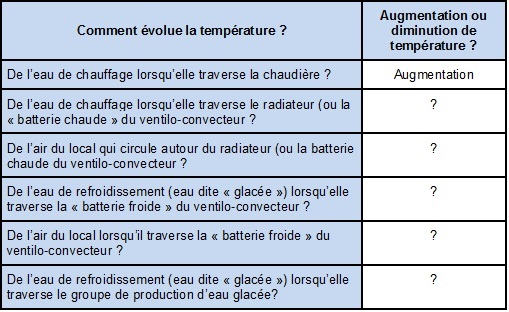
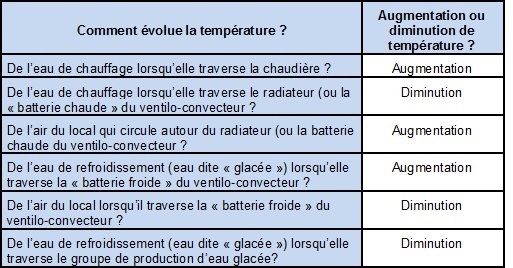
Cette formule est logique. Plus le débit d’eau q_v est important, plus la puissance (de chauffage ou de refroidissement) véhiculée est a priori importante. Mais à elle seule, l’importance du débit n’est pas en soit suffisante pour juger de la puissance (de chauffage ou de refroidissement) distribuée. Ainsi on peut envoyer autant d’eau froide que l’on voudra dans un radiateur, il ne chauffera pas plus...
Pour qu’il y ait chauffage ou refroidissement, il faut que l’eau en circulation cède ou reçoive de la chaleur et donc que sa température varie entre l'entrée et la sortie de l'émetteur. Un écart de température entre l'entrée et la sortie de l'émetteur (ΔT) sera le signe de la délivrance d'une puissance de chauffe ou de refroidissement.

Question

Q1 Complétez le tableau.

voir la réponse

Lorsque l’on travaille sur des chaudières ou des groupes frigorifiques, leurs puissances se calculent généralement en [kW] à partir de débits exprimés en [m³/h].

Lorsque l’on travaille sur des radiateurs ou sur des ventilo-convecteurs, le [W] et le [l/h] sont plus adaptés.
On utilisera alors la formule avec les unités suivantes.
P = q_v × 1,16 × ΔT
Avec
P en [W]
q_v en [l/h]
∆T = écart de température reçu ou perdu par l’eau en [K]