N°2 - Evolution des pertes de chaleur des bâtiments - niv. 3

On peut donc comparer les pertes de chaleur d'un bâtiment à celles d'un réservoir.

Question

Q1 A votre avis, lorsque le réservoir ci-dessus se vide, le débit de fuite au fond du réservoir est-il constant?
Augmente-t-il? Se réduit-il?

Au fur et à mesure que le réservoir se vide, le débit de fuite se réduit et bien sûr au moment précis où le réservoir sera complètement vide, le débit de fuite s’annulera.

voir la réponse

Question

Q2 En ne parlant que d’écart de pression autour du point de fuite du réservoir, sauriez-vous expliquez pourquoi le débit fuite diminue au fur et à mesure que le réservoir se vide?

Un écoulement est toujours dû à un écart de pression. L’eau s’écoule de la forte pression vers la faible pression.
L’écart de pression qui génère le débit de fuite est dû à la présence d’une pression considérée comme nulle à l’extérieur du réservoir et d’une pression au fond du réservoir due au poids de l’eau qu’il contient.
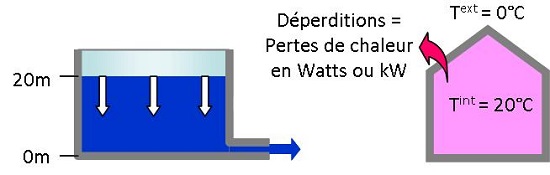
Evidemment au fur et à mesure que le réservoir se vide, la pression au fond du réservoir diminue, puisque la hauteur d'eau diminue elle aussi, ce qui a pour conséquence la diminution du débit de fuite.
C'est donc la pression en A, au fond du réservoir en image ci-dessous, qui génère le débit de fuite. Moins cette pression est importante, plus faible est le débit.
Cette pression se calcule habituellement en [bar] et elle est proportionnelle à la hauteur d'eau au-dessus de la fuite. Un bar correspond à une hauteur de 10 mètres d'eau. La pression en A est donc pour les 3 schémas ci-dessous,

p_A = 2 [bar] dans le réservoir du haut

p_A = 1 [bar] dans le réservoir du milieu

p_A = 0,5 [bar] dans le réservoir du bas

En conséquence, le débit de fuite diminue en même temps que la hauteur d'eau.

Remarque
En réalité, l’évolution du débit de fuite ne sera pas celle indiquée ci-dessus. En effet, le débit de fuite ne se réduira pas de façon proportionnelle au niveau d'eau, et les valeurs de débit indiquées n'ont pour but que de nous aider à comprendre l'évolution générale.

voir la réponse

Plus le réservoir est plein, plus les pertes d'eau sont importantes.

Visualisez la vidéo.

Les vidéos récapitulatives de Maurice.

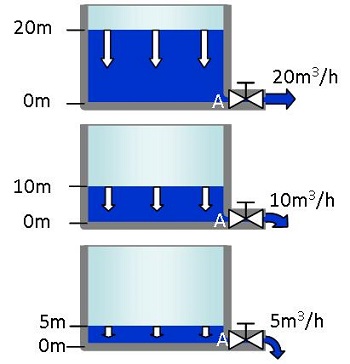
De la même façon, les pertes de chaleur d’un bâtiment diminuent au fur et à mesure que la température du local baisse.

De manière plus précise, on voit sur le schéma ci-dessus que les pertes de chaleur (déperditions) diminuent avec l'écart de température entre l'intérieur et l'extérieur du bâtiment.

Au final, on pourra donc retenir que les pertes de chaleur d'un bâtiment évoluent proportionnellement avec l'écart de température intérieur/extérieur.

Question

Q3 Compte tenu de la proportionnalité évoquée ci-dessus, en calculant les écarts de températures entre l'intérieur et l'extérieur, expliquez pour quelles raisons les déperditions de la maison ci-dessus sont successivement passées de 10 [kW] à 5 [kW], puis à 2,5 [kW].

Les déperditions sont proportionnelles à (varient comme) l'écart de température entre l'intérieur et l'extérieur de la maison.

- Pour la maison de gauche, l’écart de température entre l’intérieur et l’extérieur est.
20 - 0 = 20 [°C] (ou 20 [K])
Les pertes sont de 10 [kW].

- Pour la maison du milieu, l’écart de température entre l’intérieur et l’extérieur s'est réduit de moitié.
Soit,
10 - 0 = 10 [°C] (ou 10 [K])
Les pertes se sont donc également réduites et ne sont plus que de 5 [kW].

- Pour la maison de droite, l’écart de température entre l’intérieur et l’extérieur s'est réduit de moitié.
Soit,
5 - 0 = 5 [°C] (ou 5 [K])
Les pertes se sont donc également réduites de moitié et ne sont plus que de 2,5 [kW].

- Bien sûr, lorsque la maison sera totalement froide à 0 [°C], les pertes seront nulles.