La fraction est un des modes de représentation de la division.
Indiquer une "fraction" sans effectuer de calcul est parfois plus parlant que ne serait le résultat de la division correspondante.
Exemple 1 On partage à parts égales entre 7 personnes, une somme de 2422 €. On peut envisager 3 solutions pour en informer les heureux bénéficiaires. Le choix de l'une ou l'autre présentation relève de différents facteurs qui ne seront pas développés ici. On visera surtout à bien comprendre la construction mathématique de ces 3 présentations.
- Solution n° 1Indiquer seulement à chacun la somme de 346 € qu’il recevra (résultat de la division 2422 ÷7). C'est la solution la plus simple mais qui donne le moins d'information.
- Solution n° 2 Indiquer à chacun la somme à partager (2422 €) et la fraction qu’il en recevra de 1/7
On suppose bien sûr que les 7 personnes sauront calculer elle-même ce qui leur reviendra.
- le nombre du haut (le numérateur) représente le nombre de part que chacun recevra (1 part des 7 parts distribuées).
- le nombre du bas (le dénominateur) représente "le nombre de parts identiques distribuées".
- Solution n°3 Indiquer à chacun sous forme d’une fraction la somme qu’il recevra soit 2422/7 Euros.
Le nombre du bas (le dénominateur) représente "le nombre de parts identiques distribuées".Cette dernière solution est la plus concentrée puisqu'elle indique d'une simple fraction la totalité des informations utiles, montant total à partager et nombre de bénéficiaires.

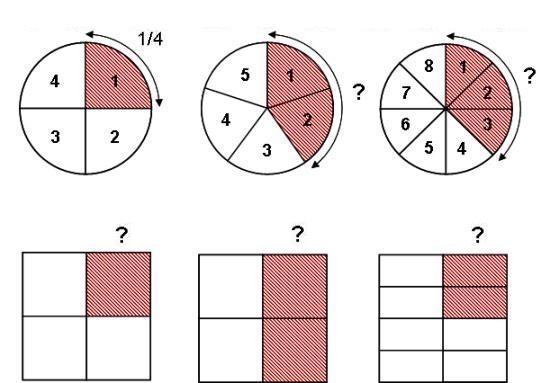
Exemple 2 On partage de manière égale un gâteau entre 4 personnes.
- Le nombre de gâteau à partager est de 1
- Le nombre de part est de 4.
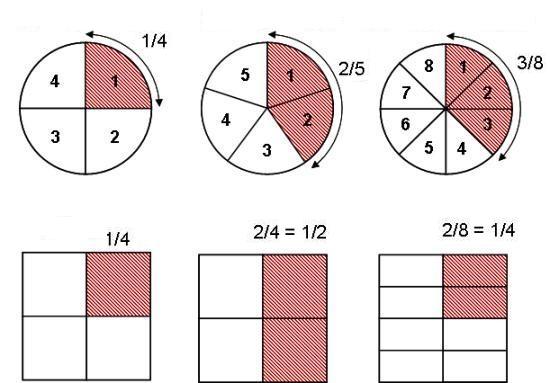
Chacun recevra 1/4 du gâteau
Dans cette fraction, le nombre du haut (le numérateur) représente le nombre de part que chacun recevra (1 part des 4 parts distribuées). Dans cette fraction de 1/4, le nombre du bas (le dénominateur) représente "le nombre total de parts identiques distribuées".
Exemple 3 On partage un gâteau en 8 parts égales.
Nous donnons,
- 1 part à Steve, il reçoit 1/8 du gâteau (1/8ème).
- 3 parts à Karim, elle reçoit 3 x 1/8 = 3/8 du gâteau (3/8ème)
Le numérateur de (3) de 3/8 représente ici le nombre de parts reçues par Karim, et le dénominateur le nombre total de parts distribuées.
- 6 parts à Andie, elle reçoit 6 x 1/8 = 6/8 du gâteau (6/8ème)
Le numérateur (6) de 6/8 représente ici le nombre de part reçu parAndie, et le dénominateur (8) le nombre total de parts distribuées.
Exemple 4 On partage un gâteau de 1000 grammes, entre 4 personnes. Chacun recevra 1/4 du gâteau soit , 1000 x 1/4 = 250 g
On pouvait aussi écrire que chacun recevrait 1000/4 grammes. Le numérateur (1000) de la fraction représente le gâteau par sa masse à partager, et le dénominateur (4) le nombre total de parts distribuées.
Exemple 5
On doit répartir à part égale un terrain de 3750 m² entre 7 personnes.
On pourra indiquer à chacun qu’il recevra une superficie de 3750 x 1/7 = 3750/7.
Le numérateur de 3750/7 représente ici le terrain à partager, et le dénominateur le nombre total de parts distribuées).
Question
Chaque gâteau pèse 750 grammes.
Indiquez combien de grammes de gâteau chacun recevra.
Chacun recevra 150 g de gâteau.
Explication
Les 7 gâteaux pèsent en tout,
750 g × 7 = 5 250 g
Ils sont partagés entre 35 personnes, donc chacune obtiendra,
(750 x 7)/35 = 150 g
Question
2/9ème de sucre
1/9ème de beurre
4/9ème de farine
2/9ème de lait
Indiquez combien de grammes de sucre, beurre, farine, lait contient le gâteau.
Le gâteau contient,
250 g de sucre
125 g de beurre
500 g de farine
125 g de lait
Explication
1125 x 2/9 = 250 g
1125 x 1/9 = 125 g
1125 x 4/9 = 500 g
1125 x 2/9 = 250 g
Question
1/8 de sucre
2/8ème de beurre
3/8èmede lait
Le reste est de la farine.
Indiquez (au centième) combien de grammes de sucre, beurre, lait et farine contient le gâteau.
Le gâteau contient,
200 g de sucre
400 g de beurre
600 g de lait
400 g de farine
Explication
1600 x 1/8 = 200 g
1600 x 2/8 = 400 g
1600 x 3/8 = 600 g
Il reste 2/8 pour la farine. 8/8 - 1/8 - 2/8 - 3/8) = 2/8
1600 x 2/8 = 400 g
Nous retrouverions bien sûr le même résultat en enlevant au 1600 g qui représentent le poids total du gâteau, le poids des 3 premiers ingrédients.
1600 g - (200 g + 400 g + 600 g) = 400 g
Question
1/4 de Whisky,
1/8ème de Vodka,
1/8ème de jus d'ananas,
1/2 de coca cola.
Indiquez (au centième et avec modération) combien de centilitres de Whisky, de Vodka, de jus d'ananas et de coca cola contient la bouteille.
La bouteille de cocktail contient,
18,75 cl de Whisky,
9,37 cl de Vodka,
9,37 cl de jus d'ananas,
37,50 cl de soda.
Explication
75 x 1/4 = 18,75 cl de Whisky
75 x 1/8 = 9,375 cl de Vodka
75 x 1/8 = 9,375 cl de Jus d'ananas
75 x 1/2 = 37,50 cl de soda
Question
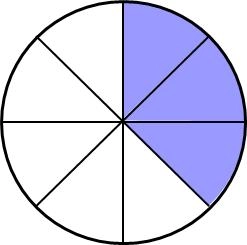
Quelle fraction du gâteau reste-il à manger pour le soir ?
Il reste 5/8 du gâteau à manger.
Explication
Midi Soir
Question
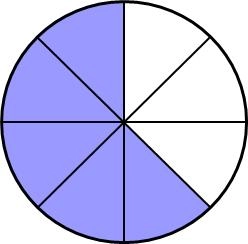
Quelle fraction du gâteau reste-il à manger pour le soir ?
Il reste 6/8 du gâteau à manger.
Explication
Petit déjeuner et déjeuner = 2/8 (= 1/4)
Soir = 6/8 (= 3/4)